马尔可夫过程

马尔可夫性质（Markov property）：一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态。

马尔可夫过程：一组具有马尔可夫性质的随机变量序列 $s_1,…,s_t$，其中下一个时刻的状态$s_{t+1}$只取决于当前状态$s_t$，离散时间的马尔可夫过程也称为马尔可夫链（Markov chain），是最简单的马尔可夫过程。

状态转移矩阵（state transition matrix）：用 来描述状态转移 $p\left(s_{t+1}=s^{\prime}\mid s_t=s\right)$

马尔可夫奖励过程

MRP (Markov reward process)= 马尔可夫过程 + 奖励函数（reward function）= 状态转移 + 奖励函数

范围（horizon）：一个回合的长度（每个回合最大的时间步数）

回报（return）：奖励的逐步叠加，也称折扣回报，其中 $γ$ 是折扣因子（超参数）

$$G_t=r_{t+1}+\gamma r_{t+2}+\gamma^2r_{t+3}+\gamma^3r_{t+4}+\ldots+\gamma^{T-t-1}r_T$$

使用折扣因子的原因：

• 有些马尔可夫过程是带环的，它并不会终结，我们想避免无穷的奖励。
• $r_t$是对环境的建模，不一定准确，不能完全信任。
• 及时奖励更重要

状态价值函数（state-value function）：一个特定状态后续回报的期望

$$\begin{aligned} V^{t}(s)& =\mathbb{E}\left[G_t\mid s_t=s\right] =\mathbb{E}\left[r_{t+1}+\gamma r_{t+2}+\gamma^2r_{t+3}+\ldots+\gamma^{T-t-1}r_T\mid s_t=s\right] \end{aligned}$$

这是一个极其复杂的树状过程，求期望可以用蒙特卡洛方法或贝尔曼方程

贝尔曼方程

求解一个状态的V价值：

$$V(s) = \underbrace{R(s)}_{\text{即时奖励}} + \gamma \underbrace{\sum_{s' \in S} p(s' \mid s) V(s')}_{\text{未来奖励的折扣总和}}$$

写成矩阵的形式：

$$\left.\left(\begin{array}{c}V\left(s_{1}\right)\\V\left(s_{2}\right)\\\vdots\\V\left(s_{N}\right)\end{array}\right.\right)=\left(\begin{array}{c}R\left(s_{1}\right)\\R\left(s_{2}\right)\\\vdots\\R\left(s_{N}\right)\end{array}\right)+\gamma\left(\begin{array}{cccc}p\left(s_{1}\mid s_{1}\right)&p\left(s_{2}\mid s_{1}\right)&\ldots&p\left(s_{N}\mid s_{1}\right)\\p\left(s_{1}\mid s_{2}\right)&p\left(s_{2}\mid s_{2}\right)&\ldots&p\left(s_{N}\mid s_{2}\right)\\\vdots&\vdots&\ddots&\vdots\\p\left(s_{1}\mid s_{N}\right)&p\left(s_{2}\mid s_{N}\right)&\ldots&p\left(s_{N}\mid s_{N}\right)\end{array}\right)\left(\begin{array}{c}V\left(s_{1}\right)\\V\left(s_{2}\right)\\\vdots\\V\left(s_{N}\right)\end{array}\right)$$

即：

$$V = R + \gamma P V \tag{1}$$

其中R为即时奖励，此时可以得到解析解！

$$V = (I - \gamma P)^{-1}R$$

但是一个问题是这个矩阵求逆的过程的复杂度是$O(N^3)$，所以一般用迭代法求近似解：

初始化$V$后带入$(1)$式右侧 求$V’$

将$V’$重新赋值给$V$进行迭代计算，直到二者差距足够小

马尔可夫决策过程（确定性策略）

MDP = MRP + 决策（Decision）

策略：在某一个状态应该采取什么样的动作 $\pi(a\mid s)=p\left(a_t=a\mid s_t=s\right)$

当策略给定时，我们可以通过加权平均”消掉“a，使得其还原为MRP，此时可以理解为人工干预导致状态转移函数发生了变化（想象一下消掉下面备份图中的中间层），同样发生变换的还有奖励函数

Q函数：动作价值函数（action-value function）,是在某一个状态采取某一个动作，它有可能得到的回报的一个期望

$$Q(s,a)=R(s,a)+\gamma\sum_{s^{\prime}\in S}p\left(s^{\prime}\mid s,a\right)V\left(s^{\prime}\right)$$

备份图（也称为回溯图）：将未来的价值备份到黑色节点上

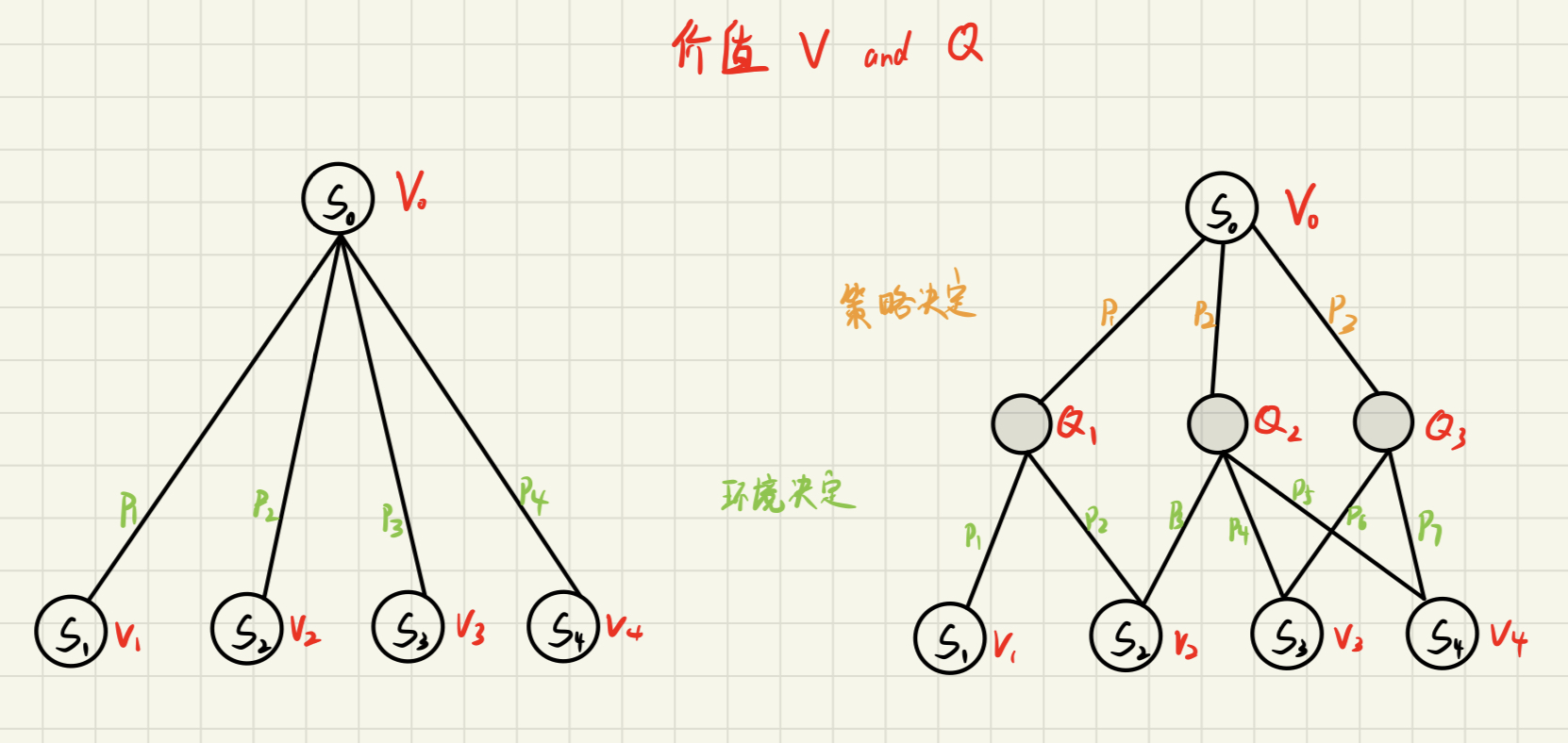
策略评估

已知马尔可夫决策过程以及要采取的策略$\pi$，计算在一个特定的状态下，我们当前采取的策略最终会产生多少价值，即计算

$$V_\pi^t(s)=\sum_ap(\pi(s)=a)\left(r(s,a)+\gamma\sum_{s'\in S}p\left(s'\mid s,a\right)V_\pi^{t-1}\left(s'\right)\right)$$

可以看出，一个状态的价值与策略有关（而不仅仅是环境的规则）。由于我们要求的是一个确定的$V_\pi(s)$，即上式中的$t->\inf$时的值，所以可以通过迭代法求解：初始化$V_0$带入上式右侧，得到$V_1$后再带入右侧直至$V_\pi(s)$收敛（用于近似t趋于无穷时的值）。

策略搜索

如何找到最佳策略，使价值函数最大化？我们可以很简单在每次选择时使用确定性策略（贪心算法）：

$$\left.\pi^*(a\mid s)=\left\{\begin{array}{ll}1,&a=\arg\max Q^*(s,a)\\0,&\text{其他}\end{array}\right.\right.$$

而计算$Q$函数还是依赖于所选择的策略，此时我们可以使用穷举：

每个状态我们可以采取 $A$ 种动作的策略，总共就是$A^S$个可能的策略。我们可以把策略穷举一遍，算出每种策略的价值函数，对比一下就可以得到最佳策略。

但这种方法太低效了，重新表述我们的问题，我们想要找到一种策略 $\pi$ 使得每个状态的价值最大：

$$\pi^*(s)=\arg\max_\pi V_\pi(s)$$

而且：对于一个事先定好的马尔可夫决策过程，当智能体采取最佳策略的时候，最佳策略一般都是确定的，而且是稳定的（它不会随着时间的变化而变化）。但最佳策略不一定是唯一的，多种动作可能会取得相同的价值。

策略迭代

先思考这样一个事实：虽然在备份图的形式上，V函数似乎依赖于Q函数。但实际上正好相反，根据Q函数公式，我们其实是先计算V函数再根据其计算Q函数的。而V函数的计算仅仅依赖于具体策略（暂时不考虑我们不能改变的环境），所以我们就有了：

$$制定策略 → 计算V函数 → 计算Q函数$$

此时的Q函数可以看作一个（状态 X 动作）的表格：

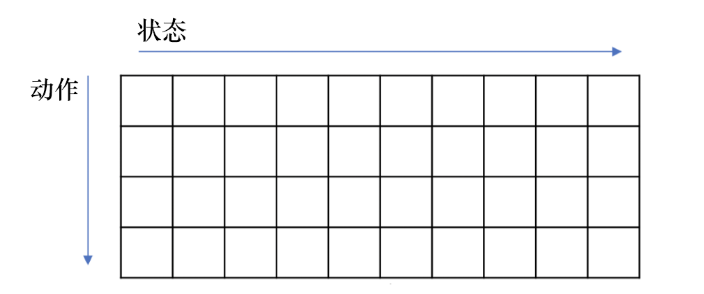
对于每个状态，我们可以直接取使它得到最大值的动作（贪心操作）：

$$\pi_{i+1}(s)=\arg\max_aQ_{\pi_i}(s,a)$$

这样就优化了我们的策略，从而又可以依照上述公式进行新的优化，形成了一个完美的闭环！

价值迭代

贝尔曼最优方程

通过上述方法不断优化策略，当其收敛后，我们就会得到一个最佳策略，此时：

每一个状态的价值必须等于在这个状态下采取最好动作得到的回报的期望

这就是 Bellman optimality equation：

$$V^*_\pi(s)=\max_{a\in A}Q^*_\pi(s,a)$$

上述的方程只有在策略收敛到最佳策略时才成立，所以V和Q都加了星号。将这个方程带入Q函数的计算方程消掉V，我们就可以得到 Q 函数之间的转移：

$$Q^*(s,a)=R(s,a)+\gamma\sum_{s'\in S}p\left(s'\mid s,a\right)\max_{a'}Q^*\left(s',a'\right)$$

同样的，我们也可以把Q函数的计算方程带入贝尔曼最优方程消掉Q得到：

$$V^*_\pi(s)=\max_a\left(R(s,a)+\gamma\sum_{s^{\prime}\in S}p\left(s^{\prime}\mid s,a\right)V^*\left(s^{\prime}\right)\right)$$

最优性原理定理（principle of optimality theorem）：个策略$\pi(a|s)$ 在状态 $s$ 达到了最优价值，也就是 $V_\pi(s)=V^*(s)$成立，当且仅当对于任何能够从$s$到达的$s’$，都已经达到了最优价值。

虽然这个规则只有在$s’$达到最优时才成立，但是我们依然可以在器不成立时不断使用它，使$V$不断收敛到最优价值：

$$V(s)\leftarrow\max_{a\in A} Q(s, a)=\max_{a\in A}\left(R(s,a)+\gamma\sum_{s'\in S}p\left(s'\mid s,a\right)V\left(s'\right)\right)$$

到最优价值后使用贪心算法得到最优策略：

$$\pi(s)=\arg\max_{a}\left[R(s,a)+\gamma\sum_{s'\in S}p\left(s'\mid s,a\right)V_{H+1}\left(s'\right)\right]$$